Πρώτοι αριθμοί : Μοτίβα κατανομής των πρώτων αριθμών – Του Νίκου Γιαννούλα

Δημοσίευση: Γιαννούλας Νίκος

Πρώτοι αριθμοί : Μοτίβα κατανομής των πρώτων αριθμών.

Προς: Την μαθηματική κοινότητα.

Ενημέρωση για την ύπαρξη μοτίβων στους πρώτους αριθμούς.

Μοτίβα κατανομής πρώτων αριθμών. Η αρχή ενός άπειρου περιοδικού μοτίβου.

 Η γενική υπόθεση έως σήμερα σχετικά με την ύπαρξη ή όχι μοτίβων στους πρώτους αριθμούς.

(Ένα από τα βασικά προβλήματα των πρώτων αριθμών είναι ότι έως τώρα δεν έχει βρεθεί ένα μοτίβο κατανομής με αποτέλεσμα να κάνουν την υπόθεση ότι δεν υπάρχει μοτίβο.   «Η μη ύπαρξη ενός μοτίβου κατανομής τους, η φαινομενική ανισορροπία κατανομής και εμφάνισής τόσο των Π.Α (πρώτων αριθμών) όσο και των διδύμων (ΔΔ) δημιουργεί την υπόθεση ως τώρα, ότι η ακολουθία των ΠΑ θυμίζει πολύ περισσότερο μια τυχαία διαδοχή αριθμών παρά μια καλά διατεταγμένη κανονικότητα. Μια υπόθεση που υιοθετούν οι αριθμοθεωρητικοί εδώ και πολλά χρόνια: Οι πρώτοι αριθμοί «συμπεριφέρονται» ως τυχαίοι αριθμοί.»

« Οι προσπάθειες μοντελοποίησης των πρώτων αριθμών με αποδεδειγμένο το γεγονός ότι οι πρώτοι αριθμοί είναι άπειροι στο πλήθος το παραπάνω ερώτημα μοιάζει σαν ένα απροσπέλαστο εμπόδιο.»

Εννοιολογικά  η λέξη μοτίβο :

1.επαναλαμβανόμενο «δομοστοιχείο».  2.Γενικό πλάνο που συνήθως αποτελείται από γεωμετρικά , αριθμητικά συναφή μέρη.»

Εξ ορισμού:

«Στα μαθηματικά πρώτος αριθμός (ή απλά πρώτος) είναι ένας φυσικός αριθμός με την ιδιότητα οι μόνοι φυσικοί διαιρέτες του να είναι η μονάδα και ο εαυτός του.  Το θεμελιώδες θεώρημα της αριθμητικής καθορίζει το βασικό ρόλο των πρώτων αριθμών στη θεωρία αριθμών: κάθε ακέραιος αριθμός του 1 μπορεί να γραφεί ως γινόμενο πρώτων κατά μοναδικό τρόπο, χωρίς να λαμβάνεται υπόψη η σειρά των παραγόντων.» Βικιπαίδεια. )

Το σύνολο των φυσικών αριθμών μέρος των οποίων είναι και οι πρώτοι αριθμοί αποτελεί ένα μοτίβο. ( άπειρο ,κβαντικό, χαοτικό, μερικοί από τους πολλούς χαρακτηρισμούς που ορίζουν την πολυπλοκότητα του σύμπαντος των πρώτων αριθμών) και επί πλέον «περιοδικό και αναλογικό» .  Και αν το άπειρο μας τρομάζει σαν μέγεθος υπάρχει και το άπειρο μικρό μοτίβο των πρώτων αριθμών που περιέχεται από το 0 – 1 , (0,000…1 έως 0,999…9), αυτό των ρητών δεκαδικών αριθμών των κλασμάτων.

Λογικά όλα τα προβλήματα που αφορούν τους πρώτους αριθμούς θα πρέπει να μπορούν να αποδειχτούν μέσα από σχέσεις αναλογίας των φυσικών αριθμών των οποίων, μικρό, ελάχιστο, απειροελάχιστο, μέρος είναι και οι πρώτοι αριθμοί .

Η «υπόθεση Ρίμαν» είναι μια εξαιρετική μέθοδος «προσέγγισης» της αναλογίας (συντελεστής μέσου όρου κατανομής) στην κατανομή των πρώτων αριθμών.

Η «εικασία Γκόλντμπαχ» αφού είναι γνωστό ότι οι άπειροι πρώτοι αριθμοί τείνουν σαν ποσοστό στο μηδέν 0,001% σε σχέση με τους σύνθετους που το ποσοστό τους τείνει στο 99,99% , όσο μεγαλώνουν οι ζυγοί αριθμοί τόσο αυξάνονται τα ζεύγη των λύσεων της εικασίας. Προφανώς κάποια αναλογική σχέση των αριθμών υπάρχει που δεν έχουμε βρεί ακόμη, ώστε σε ένα άπειρο σύνολο σύνθετων αριθμών 99,999% να μπορούν να υπάρχουν συνεχώς αυξανόμενα ζεύγη μεταξύ των άπειρων μεν αλλά ελάχιστου 0,000…1% σχεδόν μηδενικού ποσοστού των πρώτων αριθμών.

Αφού υπάρχει ο προσεγγιστικός πίνακας κατανομής του Ρίμαν , σε ένα αναλογικό σύνολο φυσικών ακέραιων αριθμών θα πρέπει να υπάρχει και ο αντίστοιχος αναλογικός άρα περιοδικός πίνακας κατανομής. Επομένως στον πραγματικό χώρο των φυσικών αριθμών , οι μη τετριμμένες ρίζες (άρρητοι αριθμοί) του Ρίμαν , θα πρέπει να είναι αναλογικοί (ρητοί αριθμοί….).

Και τα μοτίβα που παρουσιάζονται σήμερα είναι ένα επαναλαμβανόμενο δομοστοιχείο αναλογίας μεταξύ των φυσικών αριθμών και των πρώτων.

Αφού πρόκειται στην ουσία για μια αναζήτηση των σχέσεων αναλογίας, τα προβλήματα των πρώτων αριθμών θα πρέπει να είναι αλληλοσχετιζόμενα. Εξηγώντας την λύση στο ένα «περιέχεις» και ένα μέρος για την απόδειξη σε κάποιο ή κάποια άλλα. Δεν θα μπορείς να «κρυφτείς» και να παρουσιάσεις την απόδειξη στο κάθε πρόβλημα  σαν μια ξεχωριστή ενότητα  θα εμπεριέχει πληροφορίες, αποδείξεις και για τα άλλα προβλήματα. Θα είναι μια αλληλοσχετιζόμενη απόδειξη.

Όταν ορίζουμε ένα μοτίβο σαν το μεγάλο μοτίβο των πρώτων αριθμών θα πρέπει να έχει φανερές ή και συγκαλυμμένες πληροφορίες για όλα προβλήματα των πρώτων αριθμών.

1. Να είναι αυτοδημιούργητο, δηλαδή να δημιουργείται μόνο του από την επανάληψη ενός απλού αναλογικού μοτίβου αριθμών .
2. Να γεννά (βρίσκει) τους πρώτους αριθμούς.
3. Να δημιουργεί την παραγοντοποίηση των σύνθετων αριθμών.
4. Να μας δίνει πληροφορίες και τα μοτίβα αν υπάρχουν και ισχύει η «εικασία Γκόλντμπαχ».
5. Να μας δίνει πληροφορίες ή και να μας δείχνει αν υπάρχουν, που βρίσκονται στο μοτίβο οι άπειρες «μη τετριμμένες ρίζες της υπόθεσης Ρίμαν».
6. Να δείχνει πως σχηματίζεται αν υπάρχει ο «περιοδικός πίνακας κατανομής των πρώτων αριθμών» και που αλλάζει τιμές αφού είναι περιοδικός.
7. Να μας δίνει ή να συνεπάγονται πληροφορίες για όλα τα προβλήματα που αφορούν τους πρώτους αριθμούς.

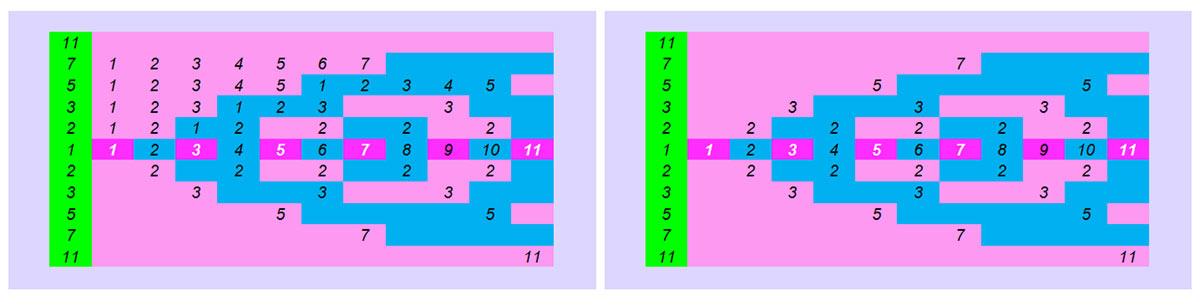
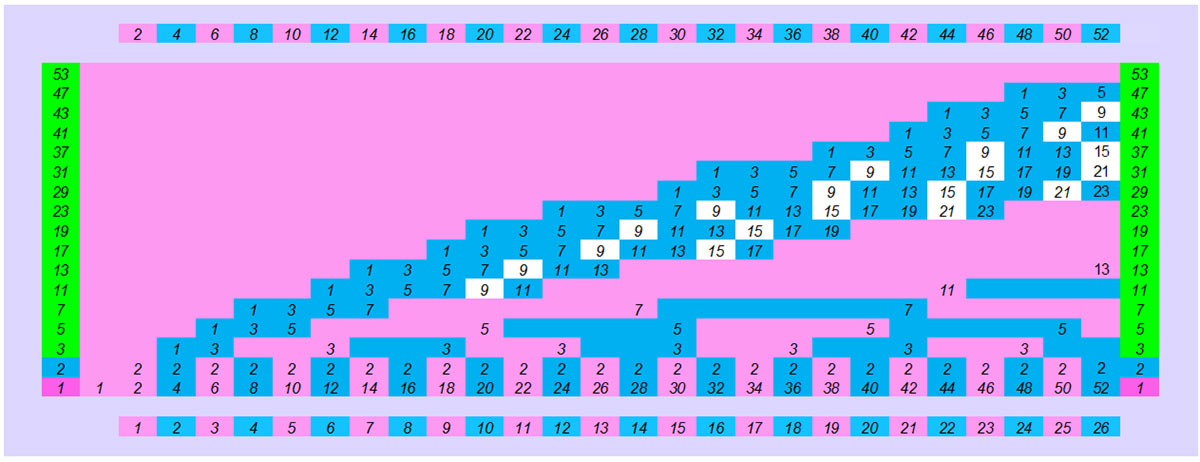
Δομή του μοτίβου των πρώτων αριθμών

Η βασική δομή του μεγάλου μοτίβου των πρώτων αριθμών.

1. Στον οριζόντιο άξονα όλοι οι φυσικοί αριθμοί 1,2,3,4,5…. Με ροζ χρώμα όλοι οι μονοί αριθμοί και με μπλε όλοι οι ζυγοί αριθμοί.
2. Στον κατακόρυφο άξονα όλοι οι πρώτοι αριθμοί. Είναι μια συνεχής επανάληψη του μεγέθους κάθε πρώτου αριθμού. Τα μονά πολλαπλάσια των πρώτων αριθμών (1Χ3,3Χ3,5Χ3…1Χ5,3Χ5, κλπ) που μας δίνουν μονούς αριθμούς με ρόζ χρώμα και τα ζυγά πολλαπλάσια τους που μας δίνουν ζυγούς αριθμούς  με μπλε χρώμα (2χ2,4χ2… 2χ3,4χ3… 2χ5,4χ5). Έτσι πέρα από το αριθμητικό μοτίβο έχουμε ταυτόχρονα και το οπτικό, γεωμετρικό μοτίβο.
3. Στον οριζόντιο άξονα των φυσικών αριθμών όταν το τέλος του μοτίβου ή των μοτίβων των πρώτων αριθμών του κατακόρυφου άξονα κατά την συνεχή επανάληψη τους συμπίπτουν (τελειώνουν) αριθμητικά και (χρωματικά) σε κάποιον αριθμό αυτός ο αριθμός είναι σύνθετος. 4,6,8,9,10. Αν δεν συμπίπτει το τέλος των επαναλαμβανόμενων μοτίβων των πρώτων αριθμών του κατακόρυφου άξονα με κάποιον αριθμό του οριζόντιου άξονα τότε είναι πρώτος αριθμός 2,3,5,…11. Τα μοτίβα του κατακόρυφου άξονα των πρώτων αριθμών κατά τα γνωστά για να προσδιορίσουν αν ένας αριθμός είναι πρώτος, επαρκούν τα μοτίβα έως την √ του κάθε φυσικού αριθμού του οριζόντιου άξονα.
4. Στο κάτω μέρος του σχήματος το αντίστοιχο συμμετρικό μοτίβο.

Στα μοτίβα παραπάνω που στο τέλος κάθε μοτίβου 3,5,7 γράφουμε τον αριθμό γιατί , πρώτον μας δίνει αυτόματα την παραγοντοποίηση κάθε αριθμού και δεύτερο προσδιορίζει το τέλος του μοτίβου .Έτσι στον πρώτο αριθμό 7 επειδή μεσολαβεί το ροζ μοτίβο του αριθμού 3 επειδή στον κατακόρυφο αυτό άξονα δεν υπάρχει αριθμός ή επισήμανση ότι εδώ υπάρχει το τέλος κάποιου μοτίβου ο αντίστοιχος αριθμός στον οριζόντιο άξονα είναι πρώτος αριθμός. Στον σύνθετο αριθμό 9 το 3 προσδιορίζει την παραγοντοποίηση του 9 αλλά και ότι σε αυτό τον αριθμό καταλήγει και το μοτίβο του αριθμού 3 οπότε είναι σύνθετος.

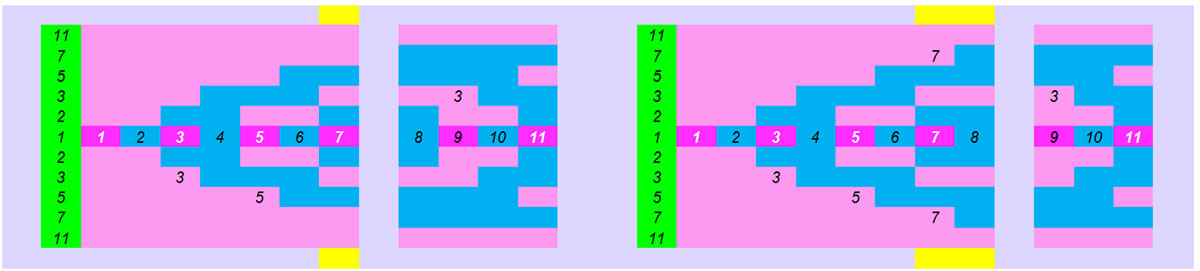
Κάτω σχήμα μοτίβο αποκλειστικά οπτικό χωρίς επισημάνσεις. Για να προσδιοριστεί αν ένας αριθμός είναι πρώτος επειδή είναι εντελώς μηχανικός ο τρόπος αναγνώρισης του μοτίβου , δεν αρκεί η μία μόνο κατακόρυφη στήλη π.χ του 7. Γιατί περνούν και άλλα δυο ροζ μοτίβα που δεν βλέπουμε αν τελειώνουν στον 7 ή συνεχίζουν. Αν όμως χρησιμοποιήσουμε πάντα και το επόμενο μοτίβο (μονό ή ζυγό) τότε βλέπουμε  πως το μοτίβο του 3 συνεχίζει και τελειώνει στο 9. Επομένως στον 7 δεν καταλήγει κάποιο μοτίβο άλλου αριθμού ,άρα είναι πρώτος. Άρα οπτικά και μόνο «μηχανικά» μπορούμε να βρούμε αν ένας αριθμός είναι πρώτος από ένα μόνο ,ίδιο παντού οπτικό μοτίβο.

Αυτό σημαίνει πως και μια μηχανή μπορεί να διακρίνει ένα απλό γεωμετρικό , αριθμητικό μοτίβο και να βρίσκει ποιος αριθμός είναι πρώτος αριθμός και ποιος είναι σύνθετος.

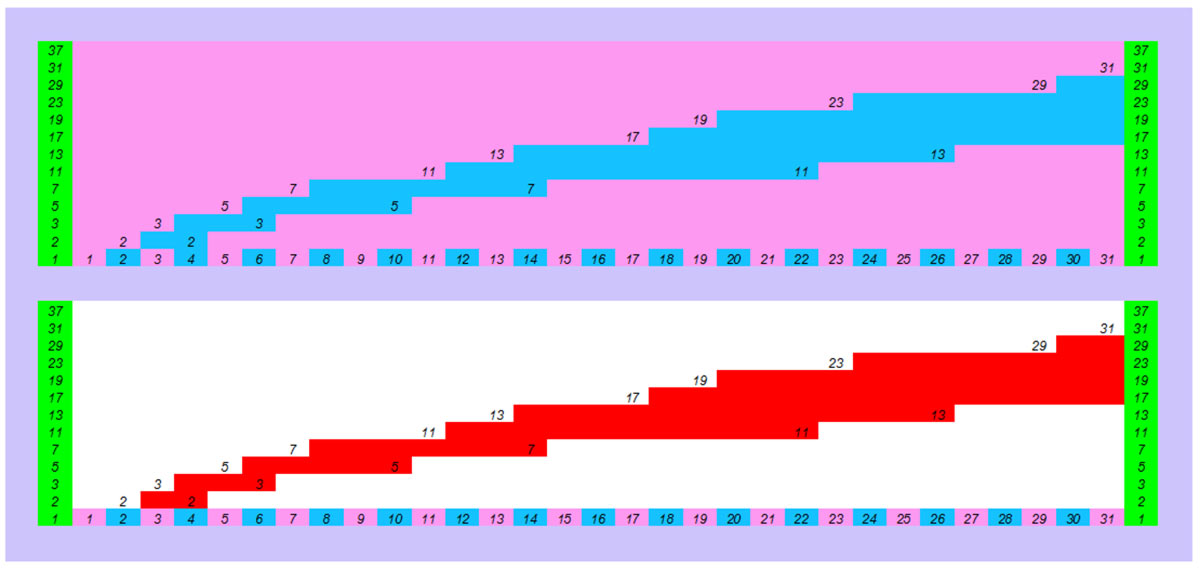
Το μεγάλο μοτίβο των πρώτων αριθμών

Εξηγήσαμε πως δημιουργείται το μεγάλο μοτίβο και πως ξεχωρίζει τους πρώτους αριθμούς από τους σύνθετους. Αν προσθέσουμε και τις πληροφορίες που υπάρχουν στο μοτίβο αλλά δεν είναι άμεσα ορατές τότε διακρίνουμε πλήθος πληροφοριών που μας εξηγούν την πολύπλοκη δομή των πρώτων αριθμών.

Αυτοτροφοδοτούμενο μοτίβο πρώτων αριθμών.

1. Για να δημιουργήσουμε το μοτίβο τοποθετούμε στον οριζόντιο άξονα όλους τους φυσικούς αριθμούς και στον κατακόρυφο άξονα μόνο πρώτους αριθμούς. Αυτούς τους πρώτους αριθμούς που χρειαζόμαστε τους βρίσκει πρώτα το μοτίβο στον οριζόντιο άξονα των φυσικών αριθμών και μετά τους τοποθετεί στον κατακόρυφο άξονα για να βρούμε τους επόμενους μετά τους επόμενους κ.λ.π. Δηλαδή πρώτα βρίσκει τους πρώτους αριθμούς που χρειάζεται ώστε μετά να τους προσθέσει σε ένα (εκθετικά αυξανόμενο) νέο μοτίβο .
2. Βρίσκει τους πρώτους αριθμούς.
3. Αν προσθέσουμε στο τέλος των επαναλαμβανόμενων μικρών μοτίβων των πρώτων αριθμών τον αριθμός τους τότε η επανάληψη τους δημιουργεί και την ταυτόχρονη παραγοντοποίηση όλων των αριθμών μονών – ζυγών.

4. Αν περιορίσουμε το μοτίβο στους 4 πρώτους αριθμούς.(2,3,5,7) χωρίς να γνωρίζουμε ότι είναι πρώτοι αριθμοί. Με βάση τα παραπάνω. Το μοτίβο του 2 συμπίπτει με όλους τους ζυγούς αριθμούς οπότε όλοι οι ζυγοί είναι σύνθετοι. Δεν τους τοποθετούμε στον κατακόρυφο άξονα των πρώτων αριθμών. Μόνο το μοτίβο του 2 μας δείχνει όλους τους πρώτους αριθμούς 1-8.Δεν συμπίπτει το μοτίβο του με κανένα μονό αριθμό. Για τον αριθμό 9=3Χ3 δεν αρκεί μόνο το μοτίβο του 2 αλλά και το μοτίβο του 3 που συμπίπτει με το 9 , και που βεβαιώνει πως είναι σύνθετος αριθμός. Το μοτίβο αυτών των δύο πρώτων 2,3 μας βρίσκει όλους τους πρώτους έως και τον αριθμό 24. Στον αριθμό 25=5Χ5 πρέπει να προσθέσουμε και το μοτίβο του 5 που μας δείχνει ότι είναι σύνθετος. Από το τετράγωνο του πρώτου αριθμού 5Χ5=25 έως το τετράγωνο του επόμενου μεγαλύτερου πρώτου αριθμού 7Χ7=49 , όλοι οι υπάρχοντες πρώτοι αριθμοί βρίσκονται από το μοτίβο των 2,3,5. Στο σχήμα με λευκό φόντο τα σημεία 9,25,49 που η κατανομή των πρώτων αριθμών χρειάζεται ένα νέο μοτίβο που προστίθεται στα προηγούμενα για την εύρεση των πρώτων αριθμών.

Έτσι το αυτοτροφοδοτούμενο μοτίβο εύρεσης των πρώτων αριθμών κ.λ.π γίνεται εκθετικό ως προς την εύρεση των πρώτων αριθμών.

Άρα στο οπτικό και αριθμητικό μοτίβο συμπεραίνουμε πως «από το τετράγωνο κάθε πρώτου αριθμού έως το τετράγωνο του επόμενου μεγαλύτερου πρώτου αριθμού» αρκούν τα μοτίβα των μικρότερων πρώτων αριθμών για να προσδιορίσουν την κατανομή όλων των πρώτων αριθμών έως το τετράγωνο του μεγαλύτερου πρώτου αριθμού. Ο τρόπος να βρούμε τους πρώτους αριθμούς έως κάποιον αριθμό είναι  συνάρτηση των προστιθεμένων νέων μοτίβων των πρώτων αριθμών.

Έτσι για μεγέθη αριθμών από – έως:

1-9: Το μοτίβο του 2. Βρίσκει τους 4 πρώτους αριθμούς.

9-25: Το μοτίβο 2,3 βρίσκει  9 ΠΑ.

25-49: Το μοτίβο 2,3,5 βρίσκει  15 ΠΑ.

49-121 : Το μοτίβο 2,3,5,7  βρίσκει  30 ΠΑ. Περιοχές με λευκή επισήμανση (9,25,49). Τα μοτίβα των 4 πρώτων αριθμών (2,3,5,7)  βρίσκουν τους 30 πρώτους αριθμούς , από το 1- 121(11Χ11).

Τι συμβαίνει στο τετράγωνο κάθε πρώτου αριθμού και τα συνεχώς προστιθέμενα νέα μοτίβα δημιουργούν μια νέα κατανομή των πρώτων αριθμών. Τα τετράγωνα των άπειρων πρώτων αριθμών είναι και αυτά «άπειρα». Σε κάθε ένα από τα «άπειρα» αυτά σημεία έχουμε μια νέα κατανομή των πρώτων αριθμών. Ναι σωστά μπορείτε να υποθέσετε .

Αλλά σε αυτή την ενότητα θα ασχοληθούμε με τα μοτίβα των πρώτων αριθμών και όχι με άλλες «υποθέσεις». Εξ άλλου οι άλλες «υποθέσεις» τιμητικά τουλάχιστον θα πρέπει να έχουν την δική τους ξεχωριστή παρουσίαση. Όπως προανέφερα τα προβλήματα των πρώτων αριθμών είναι αλληλοσχετιζόμενα.

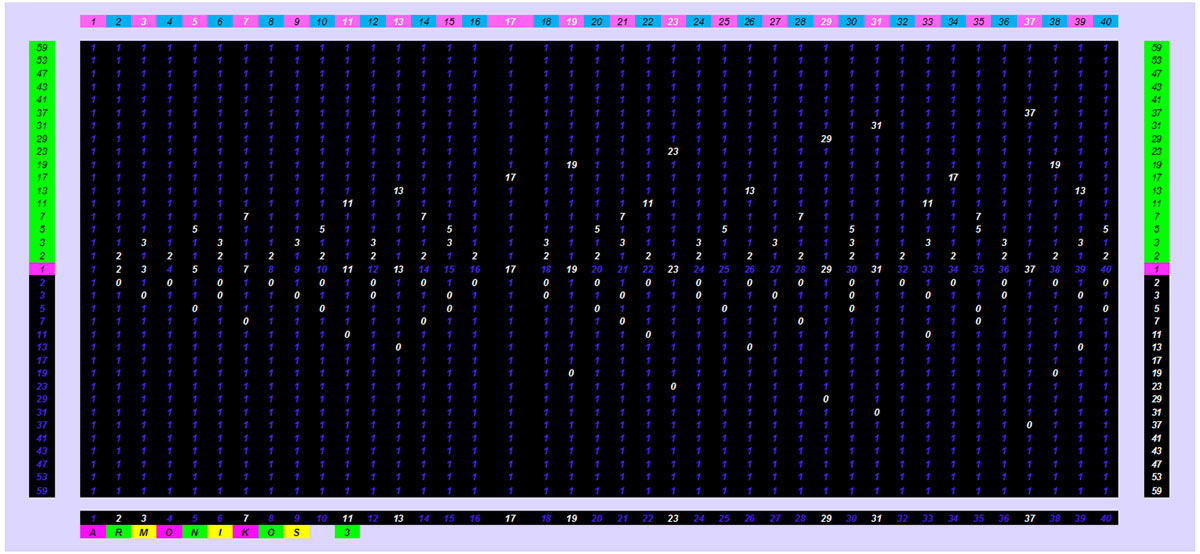
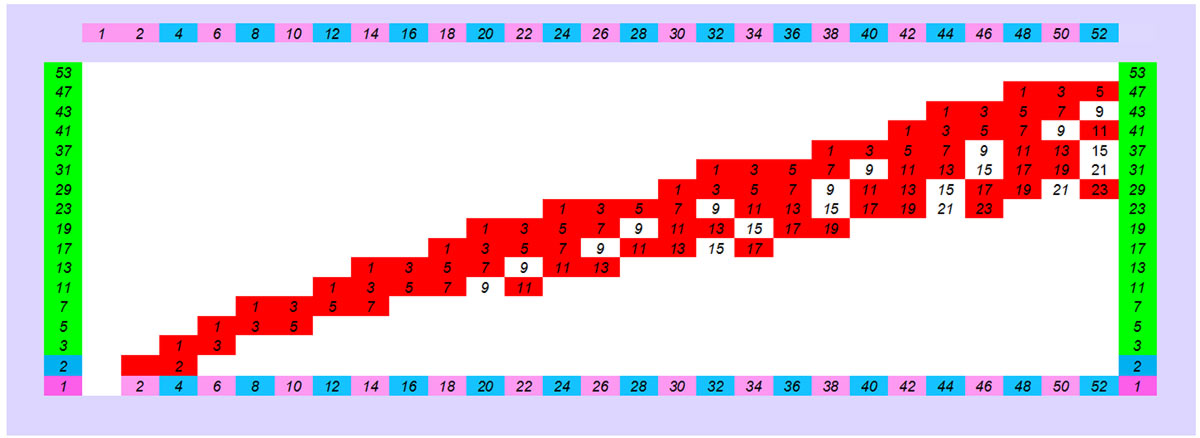
Και στο επόμενο σχέδιο το ίδιο μοτίβο σε δυαδική μορφή (0,1). Κάθε πρώτος αριθμός π.χ 11 του οριζόντιου άξονα μέχρι να συναντήσει το μοτίβου του κατακόρυφου άξονα δεν έχει στην στήλη του σύμπτωση με άλλο μοτίβο (μοτίβο είναι η ύπαρξη του αριθμού 0). Ο αριθμός 9 έχει ταυτόχρονη σύμπτωση μοτίβου με την επανάληψη του 3 , άρα σύνθετος.

Προφανώς υπάρχει και το μεγάλο μοτίβο των πρώτων αριθμών με τους μονούς μόνο αριθμούς στον οριζόντιο άξονα. Το μισό σε μέγεθος του αρχικού μεγάλου μοτίβου.

Η δομή του διαφέρει λίγο για λόγους απαραίτητα «δομικούς».

Για να διατηρήσουμε την δυνατότητα εύρεσης ενός αριθμού αν είναι πρώτος μόνο από το μοτίβο του, όπως στο μεγάλο μοτίβο θα πρέπει με ένα «τέχνασμα» να προσαρμόσουμε το μοτίβο των πρώτων αριθμών του κατακόρυφου άξονα , έτσι ώστε ,άλλοι να συμπεριφέρονται κανονικά σαν μονοί αριθμοί  και άλλοι σαν ζυγοί.  Για αυτό και τα μοτίβα των πρώτων αριθμών στον κατακόρυφο άξονα άλλα αρχίζουν με ροζ χρώμα (μονοί πρώτοι αριθμοί) και άλλα με μπλε χρώμα ( σαν ζυγοί πρώτοι αριθμοί). Επομένως το μοτίβο μόνο των μονών αριθμών παίρνει την παραπάνω ξεχωριστή δική του μορφή. Έτσι π.χ ο  σύνθετος μονός αριθμός 35 κατά την αρίθμησή του είναι μπλε (18 δηλαδή ζυγός) οπότε  στον αριθμό 35 θα συμπίπτουν τα ζυγά πολλαπλάσια των 5,7 τα μπλε δηλαδή. Επιτυγχάνουμε με αυτόν τον τρόπο και οπτική ομοιομορφία στο μοτίβο. Ο αριθμός 45 =9Χ5 μονός (ροζ) αριθμός και μονά τα πολλαπλάσια των 3,5.

Το «τέχνασμα» του μοτίβου των μονών φυσικών αριθμών .Θέλουμε να δημιουργήσουμε ένα οπτικό μοτίβο στηριζόμενο  στη ίδια σχέση (μονά-ζυγά πολλαπλάσια) εύρεσης των πρώτων αριθμών, παραγοντοποίησης,κ.λ.π  όπως στο αρχικό μεγάλο μοτίβο των πρώτων αριθμών.

1. Αριθμούμε όλους τους μονούς αριθμούς. 1,3,5,7,9=1,2,3,4,5. Όπως στο τέλος του σχήματος.
2. Οι πρώτοι αριθμοί που βρίσκονται στην αρίθμηση σε ζυγό αριθμό χρωματίζονται στην αρχή της δημιουργίας του μοτίβου, με μπλε (σαν να είναι ζυγοί), οι άλλοι με ροζ ( μονοί αριθμοί). Όταν αναπτύξουμε το μοτίβο των μονών αριθμών τότε δημιουργείται ένα μοτίβο με πρώτους αριθμούς  άλλους ροζ (μονούς) και άλλους μπλε (ζυγούς πρώτους).
3. Αν δούμε δύο συνεχόμενους πρώτους αριθμούς 17,19 βλέπουμε πως το μοτίβο τους κατακόρυφα είναι απολύτως ξεκάθαρο αν είναι πρώτοι ή όχι και είναι ίδιο με το μεγάλο μοτίβο των πρώτων αριθμών , παρόλο που οι πρώτοι αριθμοί από την αρχή του μοτίβου ξεκινούν άλλοι σαν μονοί (ροζ) και άλλοι σαν ζυγοί (μπλε).
4. Ταυτόχρονα έχουμε και την παραγοντοποίηση όλων των σύνθετων μονών αριθμών.

Εδώ γίνεται μια συνοπτικότατη παρουσίαση και δεν υπάρχει «χώρος» για όλα τα μοτίβα που συναντάμε στους πρώτους αριθμούς που το καθένα έχει την δική του χρησιμότητα.

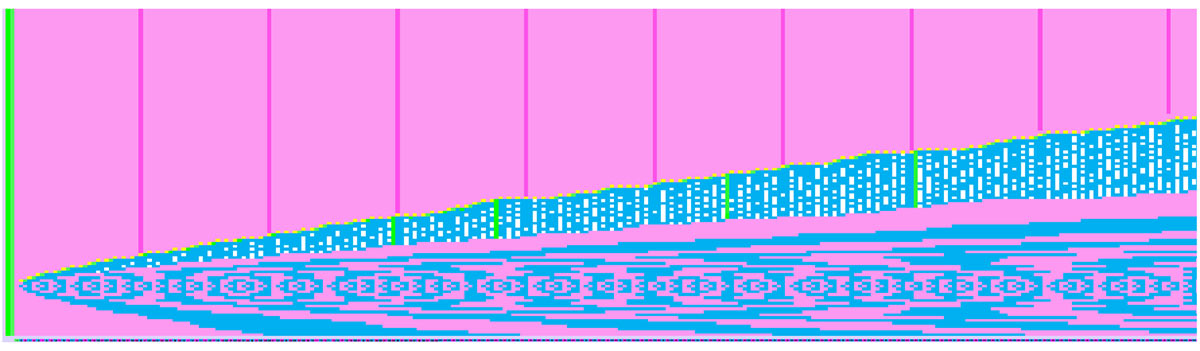
Βέβαια υπάρχει και το μεγάλο μοτίβο των ζυγών αριθμών. Εδώ είναι το ίδιο κατανοητό πλέον μοτίβο.

Ενδιαφέρον έχει πάλι η μεγάλη μπλε επιφάνεια που σχηματίζεται ξεχωριστά στο πάνω μέρος του σχήματος και στο συμμετρικό κάτω .Το ίδιο μοτίβο παρουσιάζεται και στο μεγάλο μοτίβο των πρώτων αριθμών κάτω ας το δούμε.

Το μεγάλο μοτίβο με περισσότερες πληροφορίες.

Μπορούμε στο μεγάλο μοτίβο των πρώτων αριθμών να προσθέσουμε και άλλες πληροφορίες . Αν στην μεγάλη επιφάνεια με μπλε χρώμα που σχηματίζεται στο πάνω μέρος του σχήματος  που είναι στην ουσία  τα ζυγά μοτίβα (πολλαπλάσια) των πρώτων αριθμών ( 2χ3,2χ5,2χ7) που ακολουθούν τα αρχικά (ροζ) μονά μοτίβα (1χ3,1χ5,1χ7) γράψουμε τους μονούς αριθμούς του κάθε μοτίβου (για το μοτίβο του 5 τους μονούς αριθμούς 1,3,5) τότε σχηματίζεται  το παρακάτω ενδιαφέρον μοτίβο. Με λευκή επισήμανση στη μπλε επιφάνεια οι σύνθετοι αριθμοι,9,15,κ.λ.π, όλοι οι άλλοι με μπλε είναι πρώτοι αριθμοί. Με κίτρινη επισήμανση οι ζυγοί αριθμοί του οριζόντιου άξονα. Αν προσθέσουμε και την αντιστοιχία των πρώτων αριθμών (πράσινο χρώμα) του κατακόρυφου άξονα στον κάθε ζυγό (π.χ οι 48-50 ζυγοί αριθμοί κίτρινο χρώμα) έχουμε τις συζυγίες (μονός+μονός = ζυγός) τα ζεύγη των λύσεων κάθε ζυγού αριθμού.

Βέβαια ένα μεγάλο μοτίβο πρώτων αριθμών για να ονομάζεται έτσι θα πρέπει όπως είπα στην αρχή να μας παρέχει πληροφορίες για όλα τα βασικά τουλάχιστον προβλήματα.

Το μεγάλο μοτίβο κάτω συμπυκνωμένο ώστε να διακρίνεται το μέγεθος που αρχίζει να παίρνει η ξεχωριστή αυτή μεγάλη αυτή μπλε επιφάνεια.

Η μεγάλη αυτή μπλε επιφάνεια που δημιουργείται αυτόματα ενώ εξελίσσεται το μεγάλο μοτίβο είναι η «ουρά του κομήτη Γκόλντμπαχ».

Στην ενότητα αυτή του μεγάλου μοτίβου των πρώτων αριθμών θα αναφερθούμε μόνο στα εμφανή μοτίβα που προκύπτουν και όχι στα ειδικά μοτίβα που υπάρχουν και αφορούν στα μεγάλα προβλήματα των πρώτων αριθμών.  Αν στο μοτίβο των μονών ή ζυγών αριθμών απομονώσουμε το επάνω μέρος του μοτίβου προκύπτει το σχήμα κάτω. Είναι η «ουρά του κομήτη Γκόλντμπαχ», με τις λύσεις (ζεύγη) της εικασίας.

Η «ουρά του κομήτη Γκόλντμπαχ» στο μοτίβο των ζυγών αριθμών

Με μπλε χρώμα οι αριθμοί που είναι πρώτοι και με λευκό οι σύνθετοι αριθμοί. Ο κάθε ζυγός αριθμός έχει δύο στήλες  με τις λύσεις (μονός+μονός=ζυγός)  Η μία στήλη (μπλε) που σχηματίζεται από το μοτίβο και αυτή η στήλη αντιστοιχεί σε κάποιους πρώτους αριθμούς του κατακόρυφου άξονα(πράσινη στήλη μόνο πρώτων αριθμών). Π.χ ο αριθμός 52 συντίθεται από δύο στήλες των μονών αριθμών (μπλε)+ πρώτων αριθμών(πράσινο) που αντιστοιχούν σε αυτούς τους αριθμούς (στήλη αριθμών) και το άθροισμά τους  είναι 52. 5+47=52  … 23+29=52.

Σχήμα κάτω απαλλαγμένο από της πληροφορίες μόνο η καμπύλη «ουρά του κομήτη Γκόλντμπαχ».

Η συνολική εικόνα και γνώση που έχουμε ως τώρα για την «ουρά του κομήτη Γκόλντμπαχ».

«Αν τοποθετήσουμε στον οριζόντιο άξονα συντεταγμένων της άρτιους ακεραίους και στον κατακόρυφο άξονα της δυνατούς τρόπους που μπορεί να γραφεί ο καθένας της ως άθροισμα δυο πρώτων, προκύπτει η χαρακτηριστική εικόνα «ουράς κομήτη Γκόλντμπαχ» της μπορείτε να δείτε στο παρακάτω γράφημα.
 Το 2006 άρχισαν να μελετώνται οι ιδιότητες της καμπύλης της. Είναι αξιοπρόσεκτο το γεγονός ότι oσο μεγαλύτερος ο αριθμός τόσο μεγαλύτερο το πλήθος των πιθανών ζευγών. Ο κανόνας της ισχύει σε γενικές γραμμές , αλλά όχι απόλυτα για κάθε μεμονωμένο αριθμό.»

Δεν θα το χαρακτηρίζαμε και πολύ ενημερωτικό.

Η «ουρά του κομήτη Γκόλντμπαχ» είναι ένα περιοδικό μοτίβο γεμάτο μικρά και μεγάλα επαναλαμβανόμενα μοτίβα και άλλες σημαντικές πληροφορίες .

Μια πρώτη σημαντική παρατήρηση. Η «ουρά του κομήτη Γκόλντμπαχ οριοθετείται. Το άνω όριο είναι η καμπύλη κατανομής των πρώτων αριθμών. Κάτω όριο το διπλάσιο της καμπύλης κατανομής των πρώτων αριθμών. Το διπλάσιο προφανώς καταλήγει της αντίστοιχους ζυγούς των πρώτων αριθμών,κάτω τελευταία σειρά στο σχήμα.

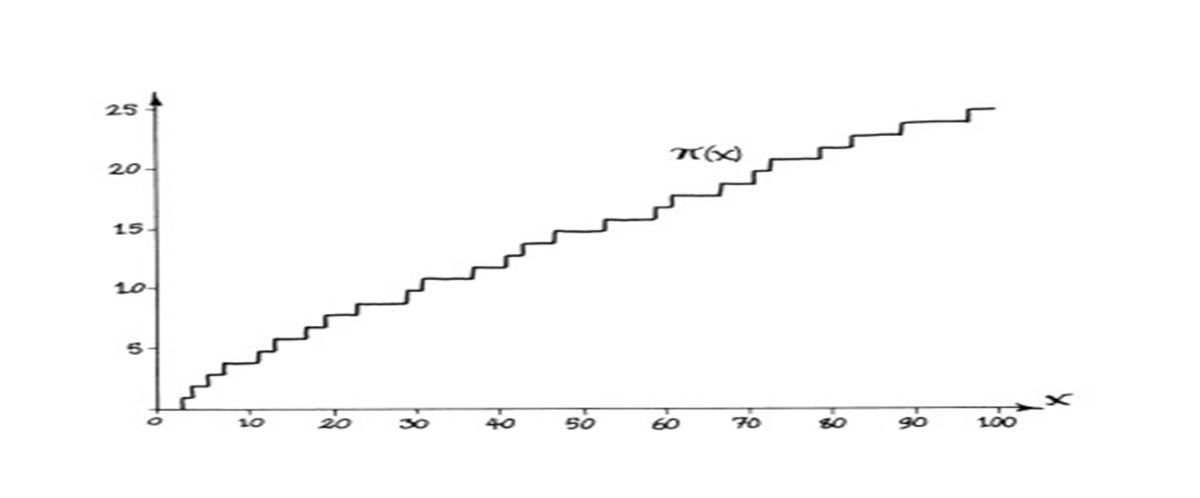
Η οριοθέτηση της επιφάνειας της «ουράς του κομήτη Γκόλντμπαχ» είναι μεταξύ « της συνάρτησης πρωταρχικής μέτρησης π (x) και του διπλασίου της»

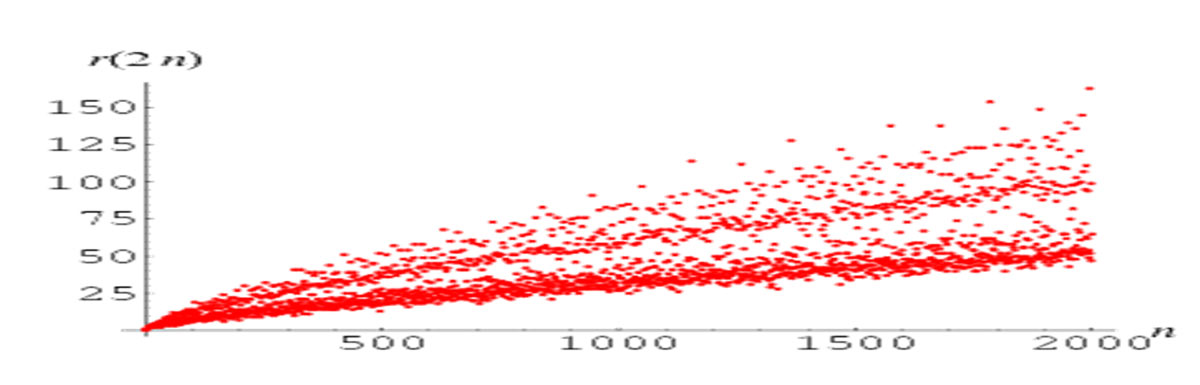
 «Η συνάρτηση πρωταρχικής μέτρησης π (x), που εισήγαγε ο Gauss, κάνει ακριβώς αυτό, δίνει τον αριθμό των πρώτων  μικρότερο ή ίσο με έναν δεδομένο πραγματικό αριθμό. Δεδομένου ότι δεν υπάρχει γνωστός τύπος για την εύρεση των πρώτων, ο πρωταρχικός τύπος μέτρησης είναι γνωστός σε εμάς μόνο ως διάγραμμα, ή η συνάρτηση βημάτων αυξάνεται κατά 1 όποτε το χ είναι πρωταρχικό. Το παρακάτω διάγραμμα δείχνει τη συνάρτηση έως x = 200.»

Η «ουρά του κομήτη Γκόλντμπαχ» σε όλη την άπειρη έκτασή της είναι ένα μεγάλο περιοδικό μοτίβο. Σε οποιοδήποτε σημείο (μέγεθος συνεχόμενων ζυγών αριθμών) υπάρχει το βασικό μοτίβο που θα αναλύσουμε παρακάτω. Υπάρχουν βέβαια τα ειδικά μοτίβα του μεγάλου μοτίβου των πρώτων αριθμών και αφορούν την «εικασία Γκόλντμπαχ», όπως και οι ειδικές αρμονικές σχέσεις των αριθμών που εξηγούν την εικασία. Επειδή όπως είπαμε τα θέματα είναι αλληλοσχετιζόμενα αυτά θα αναπτυχθούν σε ξεχωριστή δημοσίευση που θα αφορά την απόδειξη της εικασίας Γκόλντμπαχ.

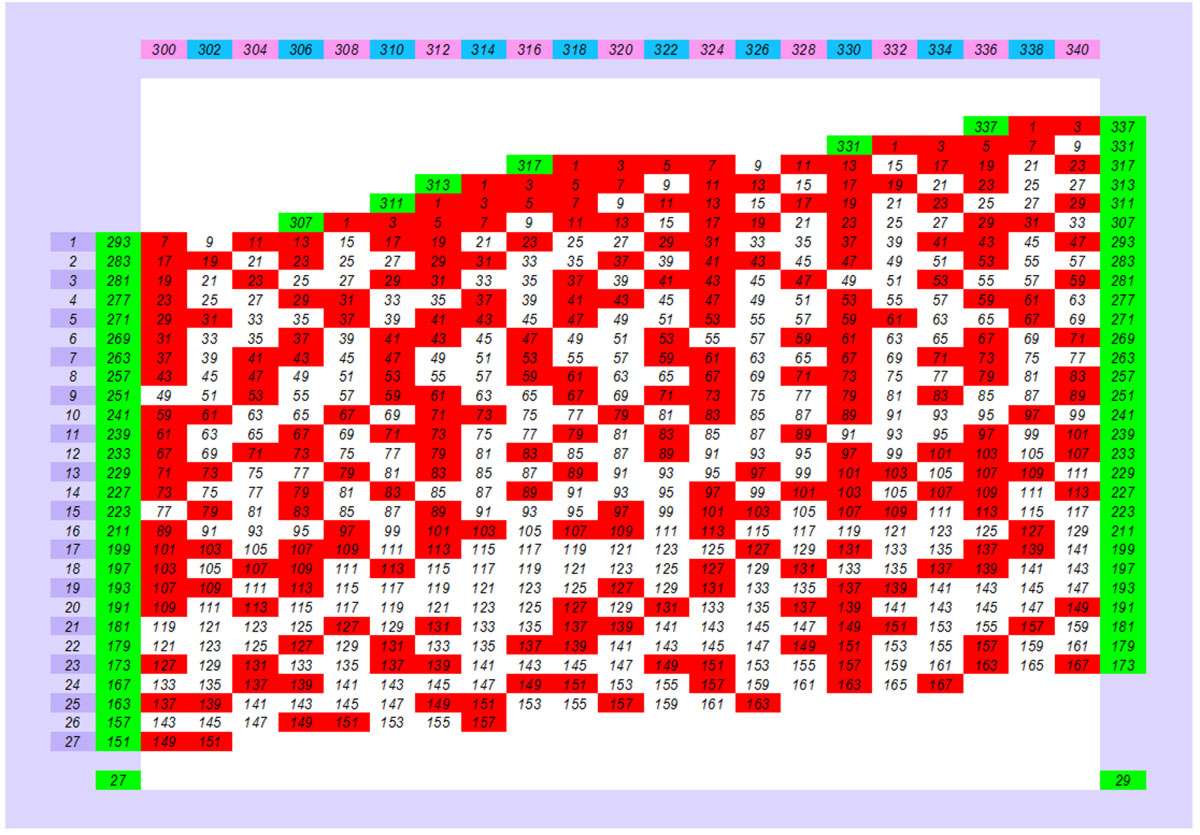
Αν πάρουμε ένα μικρό δείγμα λίγων συνεχόμενων αριθμών που έχουν αρκετές λύσεις (ζεύγη λύσεων) ,μέρος της ουράς του κομήτη Γκόλντμπαχ που σχηματίζει στην εξέλιξή το μεγάλο μοτίβο των πρώτων αριθμών,  π.χ τους ζυγούς αριθμούς από το 300 έως 340. Θα διαπιστώσουμε ότι αρχίζει να διαμορφώνεται το βασικό μοτίβο των τριών κατηγοριών που ανήκουν όλοι οι ζυγοί αριθμοί και βρίσκεται σε όλο το άπειρο σύνολο των ζυγών αριθμών. Σχήμα κάτω.

Στην πρώτη σειρά οι συνεχόμενοι ζυγοί αριθμοί 300 έως το 340.

Στην δεύτερη σειρά (μπλε) το σύνολο των λύσεων (μονός+μονός=ζυγός αριθμός) μέσος όρος 28 λύσεων. Οι ζυγοί αριθμοί είναι κοντά και  έχουν τον ίδιο πλήθος λύσεων (ζευγών) μεταξύ τους.

Στην τρίτη σειρά (κίτρινο, πράσινο ,ροζ ) οι τρεις βασικές κατηγορίες των ζυγών αριθμών που ανήκουν (ισοκατανέμονται 1/3) όλοι οι ζυγοί αριθμοί. Με το αντίστοιχο χρώμα και οι λύσεις της εικασίας Γκόλντμπαχ που έχει ο κάθε ζυγός αριθμός.

1. Επειδή και η εικασία Γκόλνμπαχ είναι πρόβλημα κατανομής των πρώτων αριθμών, σε αυτό το μέγεθος αριθμών σχηματίζονται συγκεκριμένα μοτίβα συζυγιών (μονός+μονός=ζυγός) που επαναλαμβάνονται έως το άπειρο, αλλά εδώ λόγω της κατανομής των πρώτων αριθμών περιορίζονται σε κάποιες συγκεκριμένες μορφές. Όλες αυτές οι ιδιότητες αναλυτικά  στην ενότητα της «εικασίας Γκόλντμπαχ».
2. Οι λύσεις (ζεύγη πρώτων αριθμών) της εικασίας του συνόλου των κίτρινων αριθμών «τείνουν στην ισότητα» με το άθροισμα των λύσεων των δύο άλλων (πράσινο , ροζ ) κατηγοριών των ζυγών αριθμών. Κίτρινοι=Πράσινοι+Ροζ ζυγοί αριθμοί. Αυτό το μοτίβο θα επαναλαμβάνεται συνεχώς έως το άπειρο των φυσικών αριθμών. Θα αποτελεί ένα μικρό τμήμα του συνεχώς μεταβαλλόμενου μοτίβου των ζυγών αριθμών. Αυτή η τάση προς την ισότητα εμφανίζεται σε αυτό το μέγεθος των ζυγών αριθμών , θα συνεχίσει να εμφανίζεται διαρκώς, αλλά η γενική τάση θα αλλάζει συνεχώς μέχρι να φτάσει στο ανώτατο όριο που δεν θα μπορεί να το υπερβεί.
3. Οι πράσινοι ζυγοί αριθμοί «τείνουν στην ισότητα λύσεων» με τους ροζ ζυγούς αριθμούς. Και αυτή η τάση προς την ισότητα θα υπάρχει συνεχώς σε όλο το άπειρο πλήθος των ζυγών αριθμών.
4. Αν αντιστοιχίσουμε την κάθε στήλη των ζυγών αριθμών του μοτίβου με τους αντίστοιχους (πράσινους) πρώτους αριθμούς του κατακόρυφου άξονα τότε προκύπτουν οι συνολικές λύσεις (ζεύγη) της εικασίας. Και οι λύσεις μόνο της εικασίας μεταξύ συζυγιών πρώτων αριθμών (πρώτοι αριθμοί μπλε και πράσινοι πρώτοι αριθμοί. Αντίστοιχα στο άλλο σχήμα (κόκκινοι + πράσινοι). Όπως πολύ ευκρινώς φαίνονται στον πρώτο ζυγό αριθμό (300) και στον τελευταίο (340).
5. Το μοτίβο στις εσχατιές του απείρου σύμπαντος των ζυγών αριθμών θα έχει διαμορφωθεί και θα φτάσει τα όρια του που δεν θα μπορεί να ξεπεράσει. Αυτοί οι τεράστιοι –τεράστιοι ζυγοί αριθμοί θα έχουν την οριακή τους κατάσταση που θα είναι.

Α). Αυτοί οι ζυγοί αριθμοί που θα παρουσιάζουν τις οριακές καταστάσεις, είναι συγκεκριμένοι , γνωστοί , ελάχιστοι, απειροελάχιστοι σε πλήθος αλλά άπειροι.

Β). Αυτοί οι ελάχιστοι ζυγοί αριθμοί οι μεν κίτρινοι  μειώνονται (σαν ποσοστό) σε πλήθος (ζευγών) λύσεων Γκόλντμπαχ , αλλά δεν θα πέσουν κάτω από το οριακό ποσοστό τους , όπως και δεν θα μπορούν να αυξήσουν το άνω όριο τους πάνω από ένα ποσοστό.

 Σε αυτούς τους ελάχιστους ζυγούς αριθμούς, οι πράσινοι και ροζ ζυγοί αριθμοί, αυξάνουν το ποσοστό τους σε λύσεις Γκόλτμπαχ  θα παραμένουν  σχεδόν σε σχέση ισότητας λύσεων μεταξύ τους , αλλά ταυτόχρονα θα προσεγγίζουν και το ελάχιστο ποσοστό των κίτρινων αριθμών χωρίς να τα φτάνουν καμιά φορά. Δηλαδή θα έχουμε στο ίδιο μέγεθος ζυγών αριθμών ελάχιστους ζυγούς αριθμούς και στις τρεις κατηγορίες με τις ίδιες σχεδόν λύσεις της εικασίας. Από το αρχικό μοτίβο στους αριθμούς  300-340 που οι κίτρινοι ζυγοί αριθμοί είχαν σύνολο λύσεων (κίτρινοι≈πράσινοι+ροζ), το τελικό μοτίβο διαμορφώνεται σε μια σχεδόν ισότητα , (κίτρινοι≈πράσινοι≈ροζ).

Σε αυτό το τεράστιο μέγεθος ζυγών αριθμών θα συνυπάρχουν όλα τα μοτίβα που συναντάμε από την αρχή της δημιουργίας της ουράς του κομήτη Γκόντμπαχ , αλλά λόγω της κατανομής των πρώτων αριθμών σε αυτά τα τεράστια μεγέθη που το ποσοστό ύπαρξης πρώτων αριθμών θα είναι ελάχιστο π.χ 0,005% θα έχουν διαμορφωθεί «σχεδόν» όλες οι πιθανές τάσεις που «τείνουν  τα μοτίβα του σύμπαντος» των φυσικών αριθμών. Αναλυτικά βέβαια στο μεγάλο πρόβλημα της «εικασίας Γκόλντμπαχ» που είναι αρκούντως πολύπλοκο.

Μέρος του μοτίβου της  «ουράς του κομήτη Γκόλντμπαχ» για τους συνεχόμενους ζυγούς αριθμούς από 300 έως 340

Η κάθε στήλη αντιστοιχεί σε ένα ζυγό αριθμό με μπλε χρώμα οι αριθμοί που είναι πρώτοι και με λευκό οι σύνθετοι αριθμοί. Αν την κάθε στήλη την αντιστοιχίσουμε με την στήλη (πράσινη) των πρώτων αριθμών τότε δημιουργούμε τις λύσεις της εικασίας Γκόλντμπαχ , εκεί όπου έχουμε σύμπτωση ενός μπλε (πρώτου αριθμού) και ενός πράσινου (πρώτου αριθμού) όλες αυτές οι συζυγίες είναι τα ζεύγη , οι λύσεις της εικασίας Γκόντμπαχ για τον κάθε ζυγό αριθμό.

Στην δεύτερη σειρά επάνω του σύνολο των λύσεων και από κάτω οι λύσεις της εικασίας, χωρισμένες στις τρεις κατηγορίες ζυγών αριθμών κίτρινο, πράσινο, και ροζ. Βέβαια δεν είναι ο ακριβής χωρισμός των ζυγών αριθμών σε χρώματα, αλλά υποκρύπτουν την πραγματική, αριθμητική σχέση μεταξύ των ζυγών αριθμών.  Κάτω ο ίδιος πίνακας με κόκκινη επισήμανση για να ταυτίζεται με το αρχικό σχήμα της «ουράς του κομήτη Γκόλντμπαχ».

Το ίδιο μοτίβο με κόκκινο οι λύσεις της εικασίας Γκόλνμπαχ.

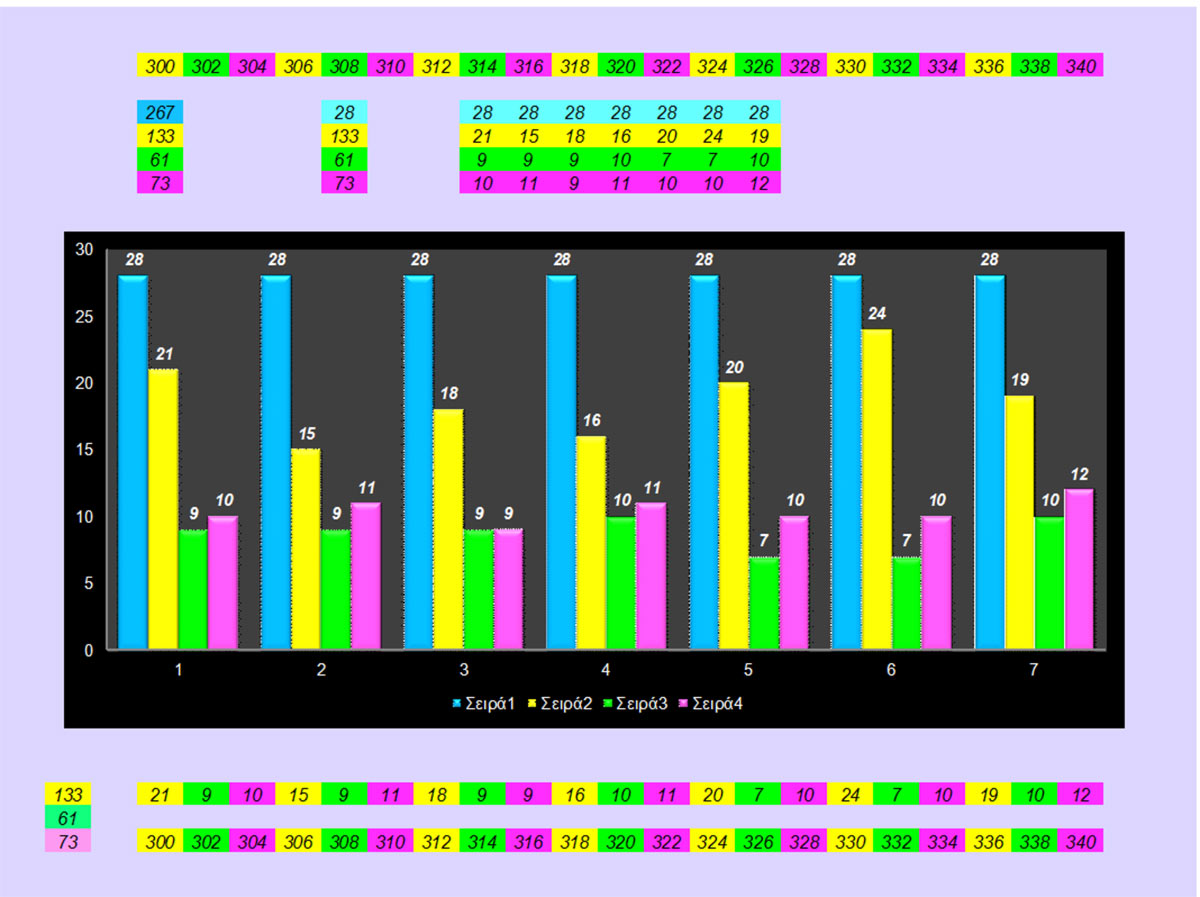
Το βασικό μοτίβο της «ουράς του κομήτη Γκόλντμπαχ» για τους ζυγούς αριθμούς στο μέγεθος των 300-340.

Αν σχηματοποιήσουμε και μεταφέρουμε τα δεδομένα από τα παραπάνω σχήματα τότε προκύπτει το ανωτέρω σχήμα.

1. Οι μπλε στήλες το σύνολο των λύσεων των ζυγών αριθμών.(μέσος όρος 28 λύσεις)
2. Οι κίτρινες στήλες με αυξημένο ποσοστό λύσεων = με το άθροισμα των δύο άλλων πράσινο και ροζ(μέσος όρος).Σε αυτό το μέγεθος αριθμών ισχύει αυτή η τάση προς ισότητα. Όσο αυξάνεται το μέγεθος των αριθμών ισχύει αυτό το μοτίβο συνεχίζει να υπάρχει στο άπειρο αλλά αυτή η τάση προς την ισότητα σαν κυρίαρχο μοτίβο μειώνεται συνεχώς καθώς εμφανίζονται και νέα μοτίβα που μας δείχνουν την τελική μορφή που θα πάρει το συνολικό μοτίβο , όπως αναφέρθηκε πιο πάνω.
3. Με πράσινο και ροζ οι στήλες των πράσινων και ροζ ζυγών αριθμών με τις λύσεις της εικασίας , που οι λύσεις των τείνουν στην ισότητα και το άθροισμά τους τείνει στην ισότητα με τις λύσεις των κίτρινων ζυγών αριθμών σε αυτό το μέγεθος αριθμών σύμφωνα με την κατανομή των πρώτων αριθμών. Αυτή είναι η εμφανής διαπίστωση που προκύπτει από το μεγάλο μοτίβο των πρώτων αριθμών και το μοτίβο της ουράς του κομήτη Γκόλντμπαχ που αυτόματα δημιουργεί, σε αυτό το μέγεθος αριθμών η  κατανομή των πρώτων αριθμών.
4. Τα υπόλοιπα ειδικά μοτίβα, σχέσεις αριθμών, οι διαφοροποιήσεις που δημιουργούνται σε αυτό το βασικό μοτίβο από τον ένα ζυγό στον άλλο ζυγό αριθμό χωρίς όμως να ανατρέπεται το αρχικό αυτό βασικό μοτίβο,αλλά συνεχώς μεταβάλλεται  είναι βασικά θέματα της «εικασίας Γκόντμπαχ» και όχι της ενότητας των μοτίβων των πρώτων αριθμών.

 «Το 2006 άρχισαν να μελετώνται οι ιδιότητες της καμπύλης της. Είναι αξιοπρόσεκτο το γεγονός ότι oσο μεγαλύτερος ο αριθμός τόσο μεγαλύτερο το πλήθος των πιθανών ζευγών. Ο κανόνας της ισχύει σε γενικές γραμμές , αλλά όχι απόλυτα για κάθε μεμονωμένο αριθμό.»

Η παρούσα δημοσίευση αποτελεί ένα μικρό τμήμα της συνολικής απόδειξης του θεωρήματος των πρώτων αριθμών.

Γιαννούλας Νίκος  3/5/2022

Στη επόμενη δημοσίευση το «ιερό δισκοπότηρο» στο θεώρημα των πρώτων αριθμών το βασικό πρόβλημα.

«Ο περιοδικός πίνακας κατανομής των πρώτων αριθμών».

«Η υπόθεση Ρίμαν συνεπάγεται αποτελέσματα για την κατανομή των πρώτων αριθμών»

Δεν έχει γίνει αντιληπτό αλλά ο περιοδικός πίνακας κατανομής των πρώτων αριθμών, αποτελεί την λύση και σε άλλες σημαντικές θεωρίες .Όπως το «φαινόμενο  της καθολικότητας», η μελέτη των αριθμών τάξης, η μοναδική πρωταρχική παραγοντοποίηση, «ιδανικοί αριθμοί» οι λογικοί αριθμοί (αριθμοί p –adic).

Όλες αυτές οι θεωρίες επιδιώκουν τον ίδιο σκοπό , να συμφιλιώσουν τους ανταγωνιστικούς πρωταρχικούς παράγοντες σε ένα μόνο σύνολο πρωταρχικών παραγόντων. Η μοναδική πρωταρχική παραγοντοποίηση είναι ένας τρόπος κατασκευής ενός αριθμητικού συστήματος από θεμελιώδη δομικά στοιχεία. Δηλαδή όπως είναι και η βάση της δημιουργίας του περιοδικού πίνακα κατανομής των πρώτων αριθμών.

Ακολουθήστε το tameteora.gr στο Google News!