Published by: Yiannoulas Nikos
To the mathematical community. Update on the existence of patterns in prime numbers.
Nino to the knowledge of the existence of patterns of distribution of prime numbers. The beginning of an infinite periodic pattern.
The general hypothesis to date about the existence or not of patterns in prime numbers.
(One of the basic problems of prime numbers is that so far a distribution pattern has not been found, leading to the assumption that there is no pattern. “The non-existence of a pattern of their distribution, the apparent imbalance of distribution and occurrence of both PAs (prime numbers) and twins (PDs) creates the assumption so far that the sequence of PAs is much more like a random sequence of numbers than a well-ordered regularity. A hypothesis that number theorists have been adopting for many years: The prime numbers “behave” as random numbers.”
“Attempts to model prime numbers with the proven fact that prime numbers are infinite in number the above question seems like an insurmountable hurdle.”
Conceptually the word pattern :
1.repeated “module”. 2.General plan usually consisting of geometric , numerically related parts.”
By definition:
“In mathematics, a prime number (or simply prime) is a natural number with the property that its only natural divisors are unity and itself. The fundamental theorem of arithmetic defines the basic role of prime numbers in number theory: any integer of 1 can be written as a product of primes in a unique way, without regard to the order of the factors.” Wikipedia. )
The set of natural numbers of which the prime numbers are a part constitutes a pattern. ( infinite , quantum, chaotic, some of the many characterizations that define the complexity of the universe of prime numbers) and furthermore “periodic and proportional” . And if infinity scares us as a quantity there is also the infinitely small pattern of prime numbers contained by 0 – 1 , (0,000…1 to 0,999…9), that of the explicit decimal numbers of fractions.
Logically all problems involving prime numbers should be provable through ratio relations of natural numbers of which, small, minimal, infinitesimal, part is also the prime numbers .
The “Riemann hypothesis” is an excellent method of “approximating” the ratio (distribution mean coefficient) in the distribution of prime numbers.
The “Goldbach conjecture” since it is known that the infinite prime numbers tend as a proportion to zero 0.001% compared to the complex ones whose proportion tends to 99.99% , as the even numbers increase the pairs of solutions to the conjecture increase. Obviously some proportional relationship of numbers exists that we have not yet found, so that in an infinite set of 99.999% complex numbers there can be ever increasing pairs between the infinite but minimal 0.000…1% almost zero percentage of prime numbers.
Since there exists the approximate Riemann distribution matrix , in a proportional set of natural integers there must also exist the corresponding proportional and therefore periodic distribution matrix. Therefore in the real space of natural numbers , the non-trivial roots (irrational numbers) of Riemann , must be analogous (explicit numbers….).
And the patterns presented today are a recurrent proportionality module between the natural numbers and the primes.
Since this is essentially a search for proportion relations, prime number problems should be interrelated. Explaining the solution to one “contains” and a part of the proof to some other(s). You will not be able to “hide” and present the proof to each problem as a separate section will contain information, proofs for the other problems as well. It will be an interrelated proof.
When we define a pattern as the great pattern of prime numbers it should have overt or covert information for all prime number problems.
1. Be self-generating, that is, self-generated by the iteration of a simple analog number pattern .
2. Generate (find) the prime numbers.
3. Generate the factorization of complex numbers.
4. To give us information and patterns if the “Goldbach conjecture” exists and is valid.
5. To give us information and or show us if there are, where in the pattern are the infinite “non-trivial roots of the Riemann hypothesis”.
6. Show how it is formed if there is a “periodic distribution matrix of prime numbers” and that it changes values since it is periodic.
7. Give or imply information about all problems involving prime numbers.
Structure of the pattern of prime numbers
The basic structure of the large pattern of prime numbers
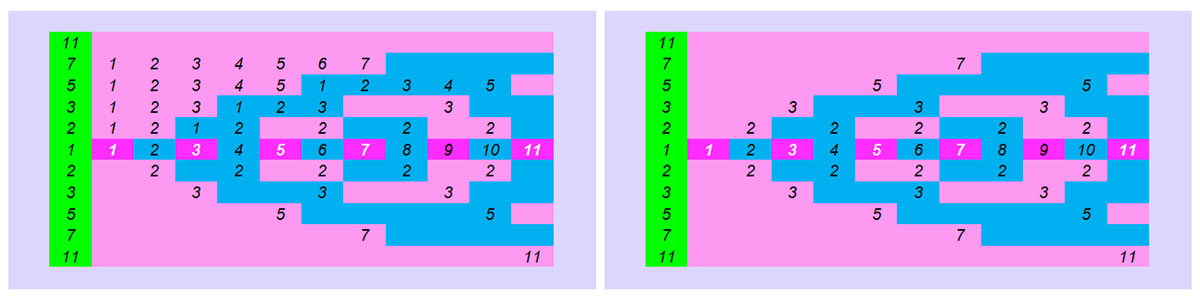
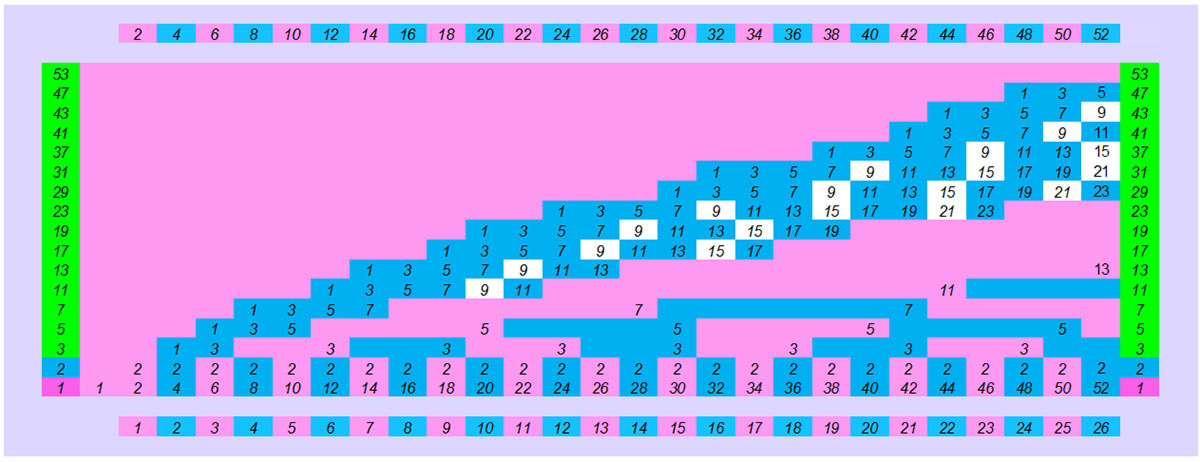
1. On the horizontal axis all the natural numbers 1,2,3,4,5…. In pink all the odd numbers and in blue all the even numbers.
2. On the vertical axis all prime numbers. It is a continuous repetition of the size of each prime number. The odd multiples of prime numbers (1X3,3X3,5X3…1X5,3X5, etc.) giving us odd numbers in pink and their even multiples giving us even numbers in blue (2×2,4×2…2×3,4×3…2×5,4×5). So in addition to the numerical pattern, we also have the visual, geometric pattern.
3. On the horizontal axis of natural numbers when the end of the pattern or patterns of the prime numbers of the vertical axis during their continuous repetition coincide (end) numerically and (chromatically) in some number this number is complex. 4,6,8,9,10. If the end of the repeating patterns of the prime numbers of the vertical axis does not coincide with a number of the horizontal axis then it is prime number 2,3,5,…11. The patterns of the vertical axis of the prime numbers as known to determine whether a number is prime, the patterns up to √ of each natural number of the horizontal axis are sufficient.
4. At the bottom of the figure the corresponding symmetrical pattern.
In the patterns above at the end of each pattern 3,5,7 we write the number because , firstly it automatically gives us the factorization of each number and secondly it identifies the end of the pattern .So in the first number 7 because the pink pattern of the number 3 is interposed on this vertical axis there is no number or indication that here is the end of a pattern the corresponding number on the horizontal axis is a prime number. In the composite number 9, 3 indicates the factorisation of 9 and also that the pattern of the number 3 ends with this number, so that it is a composite number.
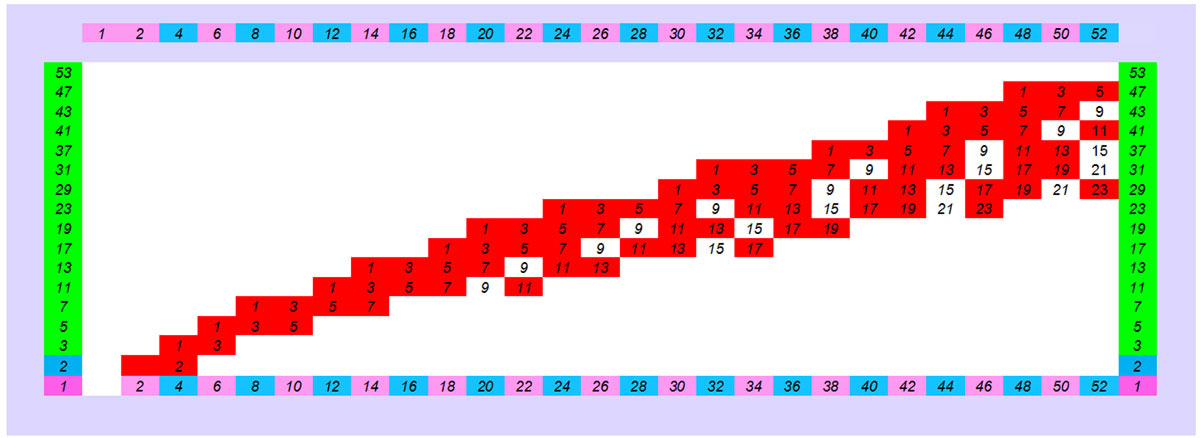
The lower figure shows a purely visual pattern without markings. In order to determine whether a number is prime because the pattern is completely mechanical, it is not sufficient to identify the pattern with only one vertical column, e.g. 7. Because two other pink patterns pass by which we cannot see whether they end at 7 or continue. But if we always use the next pattern (odd or even) then we see that the pattern of 3 continues and ends at 9. Therefore no pattern of any other number ends in 7 ,so it is first. So visually and only “mechanically” we can find out if a number is prime by a single ,same everywhere visual pattern.
This means that a machine can also distinguish a simple geometric , numerical pattern and find which number is prime and which is complex.
The large pattern of prime numbers
We explained how the large pattern is created and how it distinguishes prime numbers from complex numbers. If we add the information that is present in the pattern but not immediately visible, we can see a wealth of information that explains the complex structure of prime numbers.
Self-feeding prime number pattern.
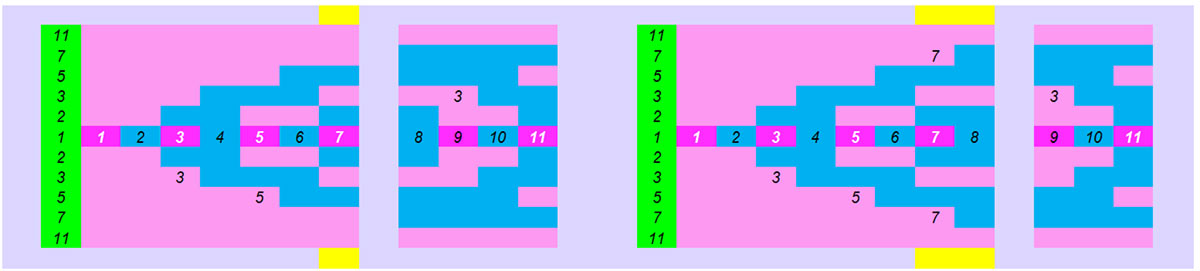
1. To create the pattern we place all natural numbers on the horizontal axis and only prime numbers on the vertical axis. These prime numbers that we need are first found by the pattern on the horizontal axis of the natural numbers and then placed on the vertical axis to find the next numbers after the next numbers and so on. That is, it first finds the first numbers it needs so that it can then add them to an (exponentially increasing) new pattern.
2. Finds the prime numbers.
3. If we add to the end of the repeated small patterns of prime numbers their number then their repetition also creates the simultaneous factorization of all odd-even numbers.
4. If we restrict the pattern to the 4 prime numbers.(2,3,5,7) without knowing that they are prime numbers. Based on the above. The pattern of 2 coincides with all even numbers so all even numbers are complex. We do not place them on the vertical axis of the prime numbers. Only the pattern of 2 shows us all the prime numbers 1-8; its pattern does not coincide with any odd numbers. For the number 9=3X3 not only the pattern of 2 is sufficient, but also the pattern of 3 which coincides with 9 , and which confirms that it is a complex number. The pattern of these two prime numbers 2,3 finds all the prime numbers up to the number 24. To the number 25=5X5 we have to add the pattern of 5 which shows us that it is complex. From the square of the first number 5X5=25 to the square of the next largest first number 7X7=49 , all existing prime numbers are found only by the pattern of 2,3,5. In the figure with white background the points 9,25,49 where the distribution of prime numbers needs a new pattern added to the previous ones to find the prime numbers.
Thus the self-sustained pattern of finding the prime numbers etc. becomes exponential in terms of finding the prime numbers. The pattern of 2,3,5,7 from 1-49.
So in the visual and arithmetic pattern we conclude that “from the square of each prime number to the square of the next largest prime number” the patterns of the smallest prime numbers are sufficient to determine the distribution of all the prime numbers to the square of the largest prime number. The way to find the prime numbers up to some number is a function of the added new prime number patterns.
So for number sizes from – to:
1-9: The pattern of 2. It finds the 4 prime numbers.
9-25: The pattern 2,3 finds 9 PAs.
25-49: Pattern 2,3,5 finds 15 PAs.
49-121 : Pattern 2,3,5,7 finds 30 PAs. Areas marked in white (9,25,49). The patterns of the first 4 numbers (2,3,5,7) find the first 30 numbers , from 1- 121(11X11).
What happens to the square of each prime number and the continuously added new patterns create a new distribution of prime numbers. The squares of infinite prime numbers are also “infinite”. At each of these “infinite” points we have a new distribution of prime numbers. Yes right you can guess .
But in this section we will deal with patterns of prime numbers and not with other “assumptions”. Besides the other “hypotheses” honorably at least should have their own separate presentation. As I mentioned before the problems of prime numbers are interrelated.
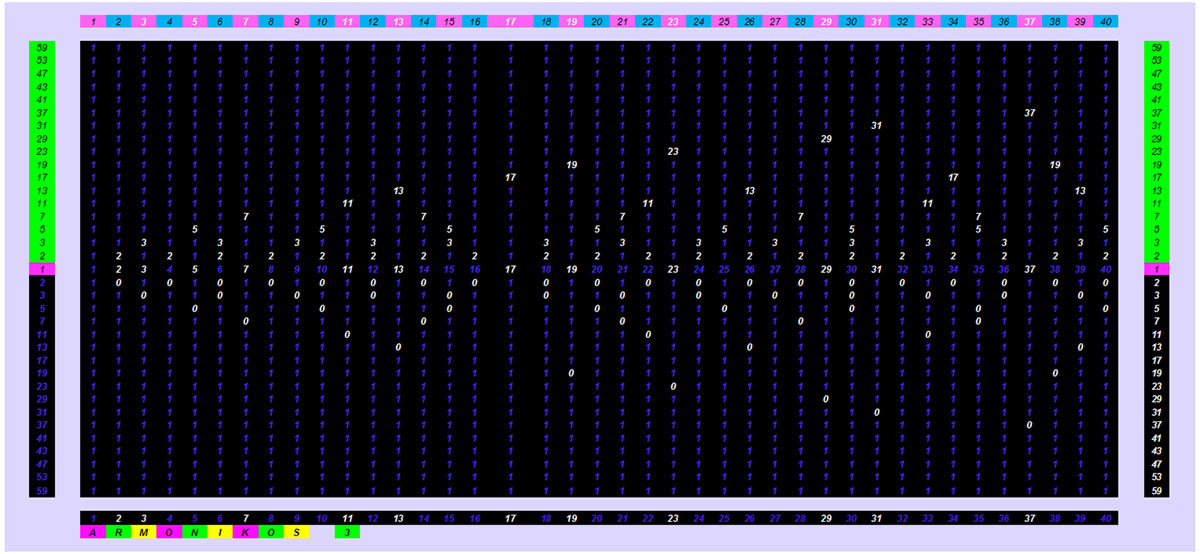
And in the next drawing the same pattern in binary form (0,1). Each prime number e.g. 11 of the horizontal axis until it meets the pattern of the vertical axis has no coincidence with another pattern in its column (pattern is the existence of the number 0). The number 9 has a simultaneous pattern coincidence with the repetition of 3 , so it is complex.
Obviously there is also the large pattern of prime numbers with only odd numbers on the horizontal axis. Half the size of the original large pattern.
Its structure differs slightly for reasons necessarily “structural”.
To preserve the possibility of finding a number if it is prime only by its pattern, as in the large pattern we have to “trick” to adjust the pattern of prime numbers on the vertical axis , so that ,some behave normally as odd numbers and others as even numbers. This is why the patterns of the prime numbers on the vertical axis sometimes start in pink (single prime numbers) and others in blue (as even prime numbers). Therefore the pattern of only the odd numbers takes the above separate form of its own. Thus, for example, the composite odd number 35 when counted is blue (18
i.e. an even number) so that the even multiples of 5.7 will coincide with the number 35, i.e. In this way we achieve visual uniformity in the pattern. The number 45 = 9X5 odd (pink) number and odd (pink) multiples of 3,5.
The “trick” of the pattern of odd natural numbers .We want to create a visual pattern based on the same relationship (odd-even multiples) of finding prime numbers, factoring,etc. as in the original large prime number pattern.
1. We count all odd numbers. 1,3,5,7,9=1,2,3,4,5. As at the end of the figure.
2. The prime numbers in the even number count are colored at the beginning of the pattern creation, in blue (as if they are even numbers), the others in pink ( odd numbers). When we develop the odd number pattern then a pattern is created with prime numbers other pink (odd numbers) and other blue (even prime numbers).
3. If we look at two consecutive prime numbers 17,19 we see that their pattern vertically is absolutely clear whether they are prime or not and is the same as the large pattern of prime numbers , even though the prime numbers from the beginning of the pattern start out some as singles (pink) and others as evens (blue).
4. At the same time we have the factorization of all complex odd numbers.
This is a very brief presentation and there is no “space” for all the patterns found in the prime numbers, each of which has its own utility.
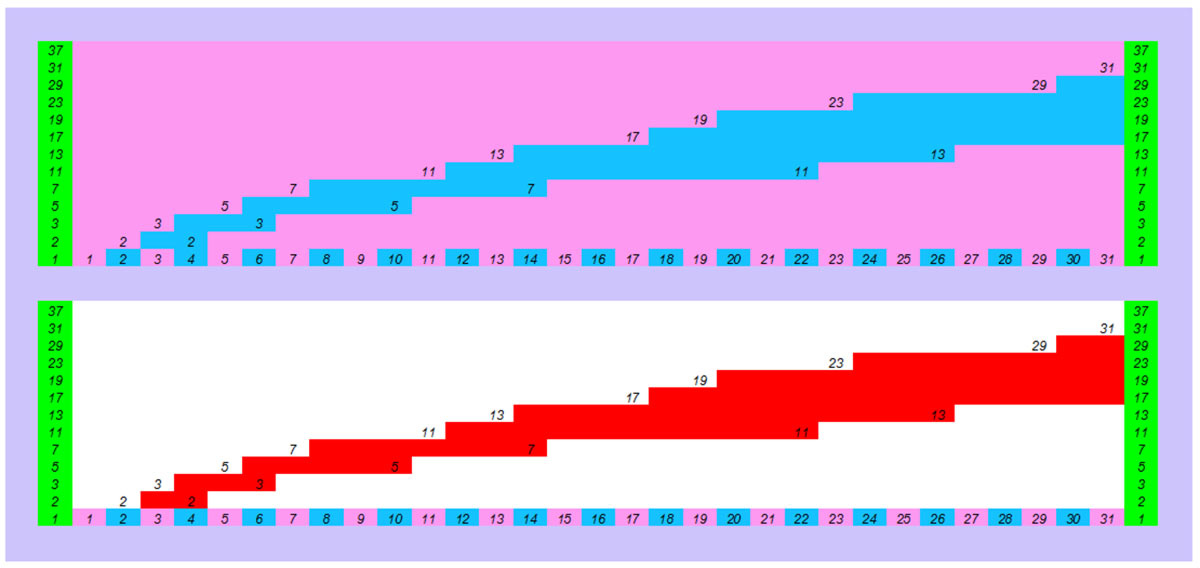
Of course there is the great pattern of even numbers. Here is the same now understood pattern.
Interesting again is the large blue surface that is formed separately at the top of the figure and the symmetrical one below .The same pattern is shown in the large pattern of prime numbers below let’s see it.
The large pattern with more information.
We can add more information to the large pattern of prime numbers . If on the large blue colored surface formed at the top of the figure which is actually the even patterns (multiples) of the prime numbers ( 2×3,2×5,2×7) following the original (pink) odd patterns (1×3,1×5,1×7) we write the odd numbers of each pattern (for the pattern of 5 the odd numbers 1,3,5) then the following interesting pattern is formed. With white highlighting on the blue surface the composite numbers,9,15,etc, all others in blue are prime numbers. Highlighted in yellow are the even numbers on the horizontal axis. If we add the correspondence of the prime numbers (green) of the vertical axis to each even number (e.g. 48-50 even numbers in yellow) we have the conjugates (odd+even = even) the pairs of solutions of each even number.
Of course, a large pattern of prime numbers to be called so should, as I said at the beginning, provide information about at least all the basic problems.
The large pattern below is condensed to show the size that this separate large blue surface is beginning to take.
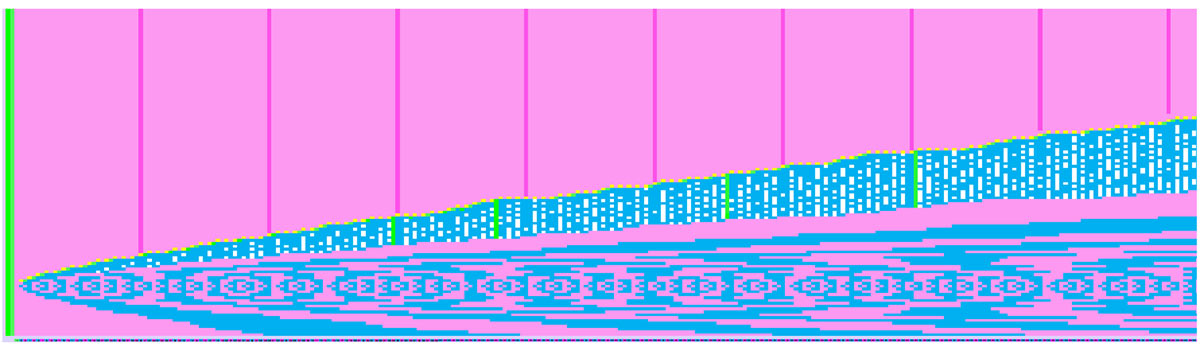
This large blue surface that is automatically created as the large pattern evolves is the “tail of the Goldbach comet”.
In this section of the large pattern of prime numbers we will refer only to the obvious patterns that emerge and not to the special patterns that exist and relate to the large problems of prime numbers. If in the pattern of odd or even numbers we isolate the upper part of the pattern the pattern below results. It is the “tail of the Goldbach comet”, with the solutions (pairs) of the conjecture.
The “tail of the Goldbach’s comet” in the pattern of even numbers
Numbers that are prime in blue and complex numbers in white. Each even number has two columns with the solutions (odd + even = even) One column (blue) formed by the pattern and this column corresponds to some prime numbers of the vertical axis (green column of only prime numbers). E.g. the number 52 is composed of two columns of odd numbers (blue)+ prime numbers(green) corresponding to these numbers (column of numbers) and their sum is 52. 5+47=52 … 23+29=52.
Figure below free of information only the “tail of the Goldbach’s comet” curve.
The total picture and knowledge we have so far about the “tail of comet Goldbach”.
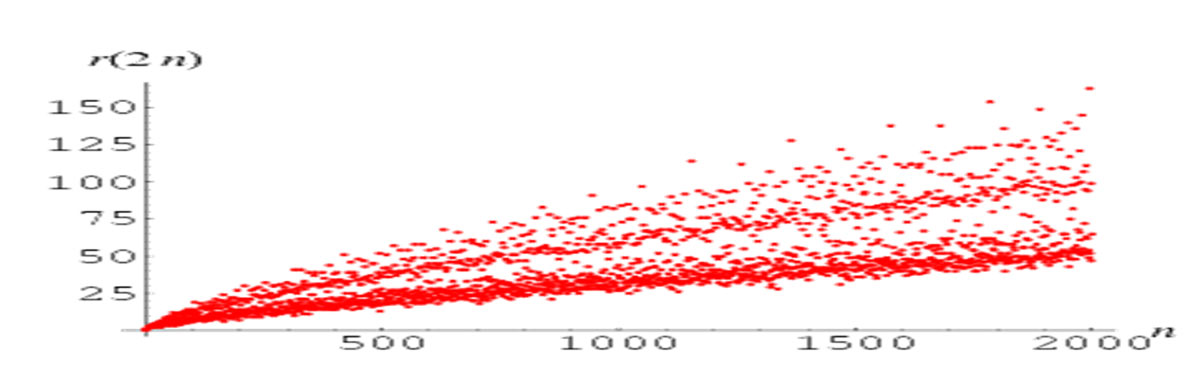
” If we place on its horizontal coordinate axis even integers and on its vertical axis possible ways that can each be written as a sum of two first ones, the characteristic picture of “tail of comet Goldbach” is obtained.
In 2006 the properties of her curve began to be studied. It is remarkable that the higher the number the larger the number of possible pairs. Her rule holds in general , but not perfectly for each individual number.”
We wouldn’t call it very informative.
The “tail of the Goldbach comet” is a periodic pattern full of small and large repeating patterns and other important information .
A first important observation. The Goldbach’s comet tail is delineated. The upper boundary is the distribution curve of prime numbers. The lower boundary is twice the prime number distribution curve. The double obviously ends up of the corresponding even number of prime numbers,bottom last row in the figure.
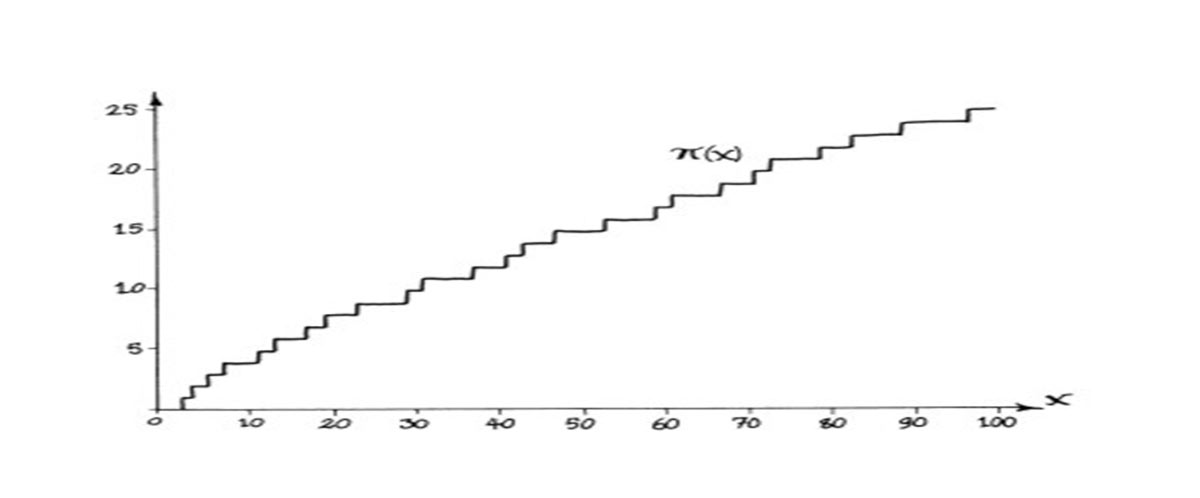
The boundary of the surface of the “tail of the Goldbach comet” is between “the prime function π(x) and its double”
“The prime counting function π (x), introduced by Gauss, does just that, it gives the number of primes less than or equal to a given real number. Since there is no known formula for finding the primes, the prime counting formula is known to us only as a diagram, or the step function is increased by 1 whenever x is prime. The diagram below shows the function up to x = 200.”
The “tail of comet Goldbach” in all its infinite extent is a large periodic pattern. At any point (size of consecutive even numbers) there is the basic pattern that we will discuss below. There are, of course, the special patterns of the large pattern of prime numbers and they relate to the “Goldbach conjecture”, as well as the special harmonic relations of the numbers that explain the conjecture. Since as we said the topics are interrelated these will be developed in a separate paper dealing with the proof of the Goldbach conjecture.
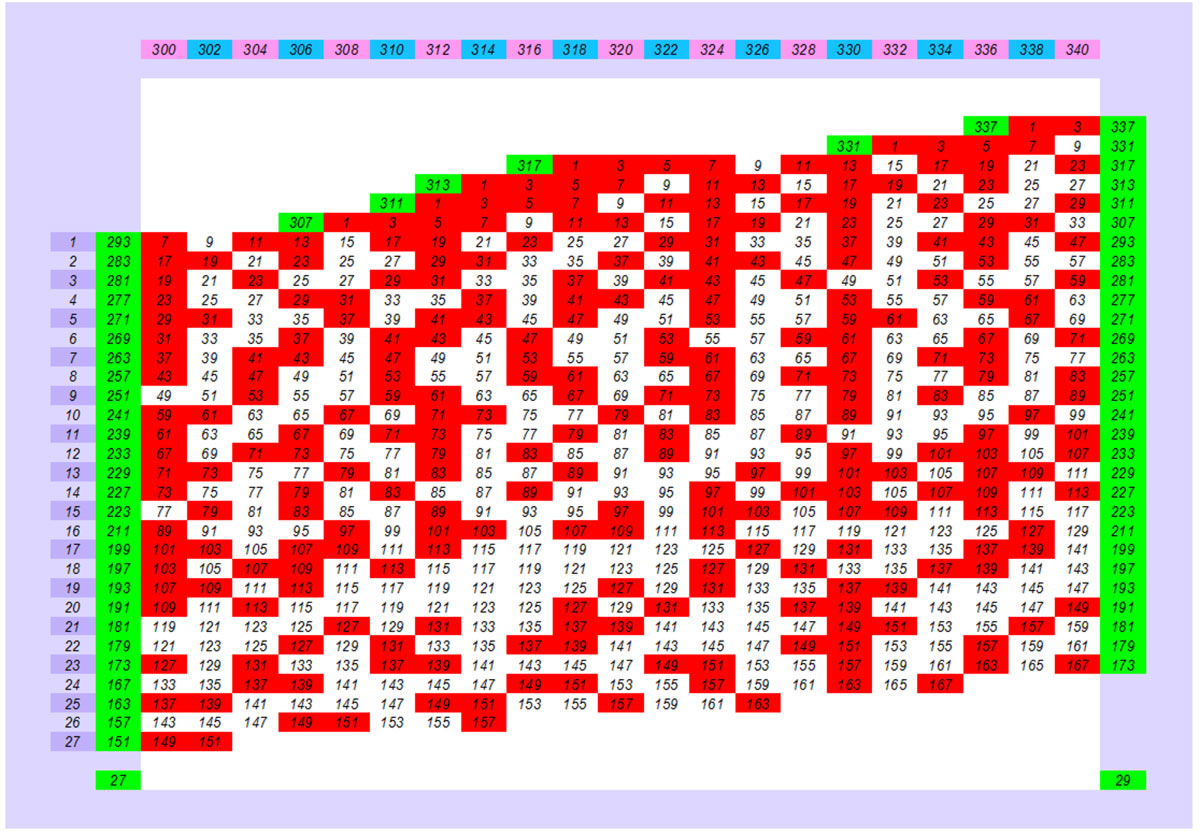
If we take a small sample of a few consecutive numbers that have several solutions (pairs of solutions) ,part of the tail of the Goldbach comet that forms in evolution the large pattern of prime numbers, e.g. the even numbers from 300 to 340. We will find that the basic pattern of the three categories to which all even numbers belong begins to form and is found throughout the infinite set of even numbers. Figure below.
In the first row the consecutive even numbers 300 to 340.
In the second row (blue) the set of solutions (odd + even = even number) averaging 28 solutions. The even numbers are close and have the same number of solutions (pairs) between them.
In the third row (yellow, green ,pink ) the three main categories of even numbers that all even numbers belong to (equal 1/3). In the corresponding color and the solutions of the Goldbach conjecture that each even number has.
1. Because the Goldbach conjecture is also a problem of distribution of prime numbers, in this size of numbers certain patterns of conjugations (odd+even=even) are formed which repeat to infinity, but here because of the distribution of prime numbers they are restricted to some specific forms. All these properties are detailed in the section on “Goldbach’s conjecture”.
2. The solutions (pairs of prime numbers) of the conjecture of the set of yellow numbers “tend to equality” with the sum of the solutions of the two other (green , pink ) categories of even numbers. Yellow=Green+Pink even numbers. This pattern will be repeated continuously to infinity of natural numbers. It will be a small part of the ever changing pattern of even numbers. This trend towards equality occurs at this size of even numbers , it will continue to occur continuously, but the general trend will change continuously until it reaches a maximum that cannot be exceeded.
3. The green even numbers “tend to solution equality” with the pink even numbers. And this tendency towards equality will exist continuously throughout the infinite number of even numbers.
4. If we match each column of even numbers in the pattern with the corresponding (green) prime numbers on the vertical axis, then the total solutions (pairs) of the conjecture are obtained. And the solutions only of the conjecture between conjugates of prime numbers (prime numbers blue and green prime numbers. Similarly in the other figure (red + green). As very clearly shown in the first even number (300) and the last one (340).
5. The pattern at the extremes of the infinite universe of even numbers will have been formed and will have reached its limits that it cannot exceed. These huge -extreme even numbers will have their limit state which will be.
A). These even numbers that will have their limit states are specific, known, minimal, infinitesimal in number but infinite in number.
B). These minimal even numbers yellow decrease (as a percentage) in number (pairs) of Goldbach’s solutions , but will not fall below their limiting percentage , just as they cannot increase their upper limit by more than a percentage.
At these minimum even numbers, the green and pink even numbers, increasing their percentage of Goldbach’s solutions will remain almost in a solution equality relationship with each other , but at the same time they will approach the minimum percentage of yellow numbers without reaching them at any time. That is, we will have in the same size of even numbers minimum even numbers in all three categories with almost identical solutions of the conjecture. From the initial pattern in the numbers 300-340 where the even numbers had a set of solutions (yellow≈green+pink), the final pattern is formed to a near equality , (yellow≈green≈pink).
In this huge size of even numbers all the patterns that we have encountered since the beginning of the formation of the tail of the Godbach comet will coexist , but because of the distribution of prime numbers in these huge sizes where the percentage of prime numbers existence will be minimal e.g. 0.005%, “almost” all possible trends that “tend the patterns of the universe” of natural numbers will have been formed. In detail of course in the big problem of the “Goldbach conjecture” which is sufficiently complex.
Part of the “Goldbach’s comet tail” pattern for consecutive even numbers from 300 to 340
Each column corresponds to an even number, with prime numbers in blue and composite numbers in white. If we match each column with the column (green) of prime numbers then we generate the solutions of the Goldbach conjecture , where we have a coincidence of a blue (prime number) and a green (prime number) all these conjugations are the pairs , the solutions of the Godbach conjecture for each even number.
In the second row above the set of solutions and below the solutions of the conjecture, divided into the three categories of even numbers yellow, green, and pink. Of course, this is not the exact division of even numbers into colors, but they conceal the actual, numerical relationship between the even numbers. Below is the same chart with red highlighting to match the original shape of the “tail of the Goldbach comet”.
The same pattern in red the solutions to the Goldbach conjecture.
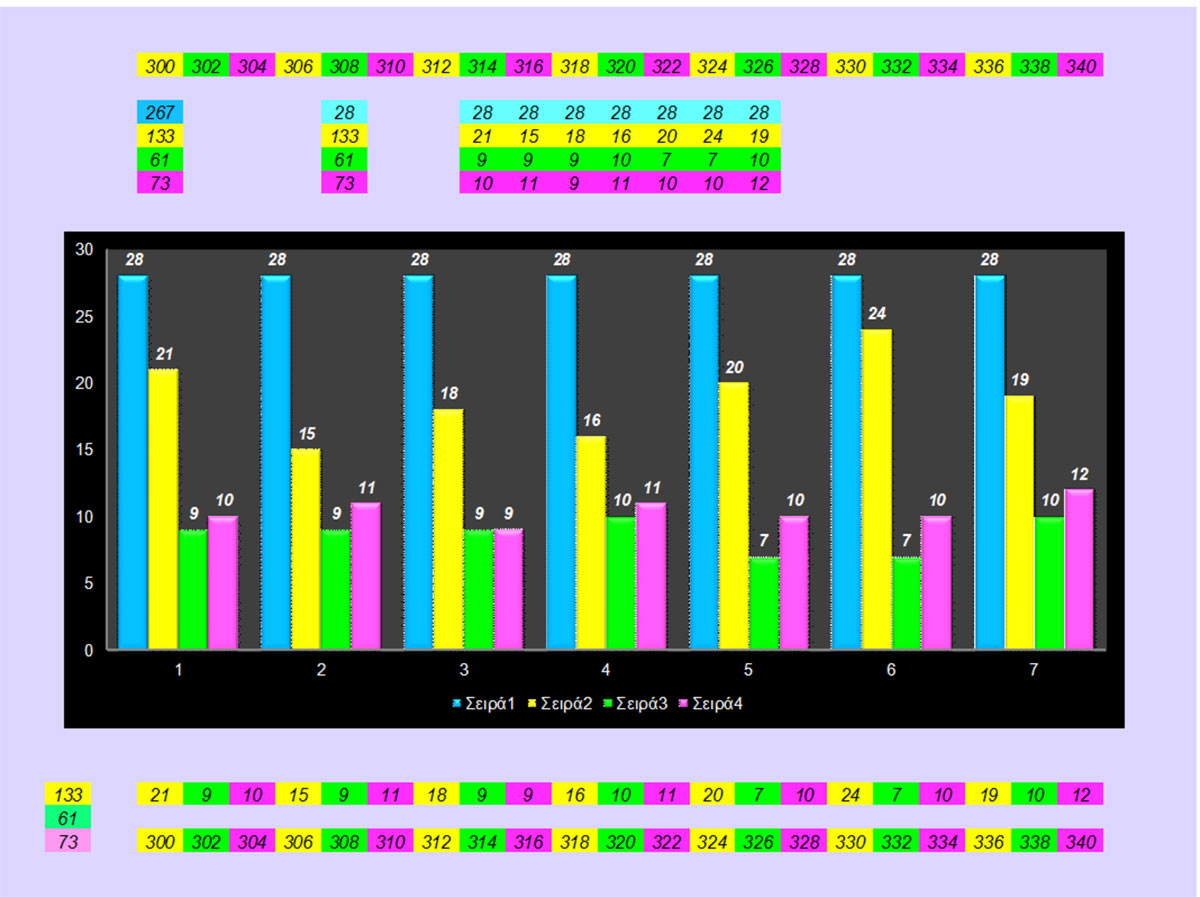
The basic pattern of the “Goldbach’s comet tail” for the even numbers in the 300-340 range.
If we format and transfer the data from the above figures then the above figure is obtained.
1. The blue columns are the set of solutions of the even numbers (average 28 solutions).
2. The yellow columns with an increased percentage of solutions = with the sum of the other two green and pink(average).At this size of numbers this tendency towards equality applies. As the number size increases this pattern holds true at infinity but this tendency towards equality as the dominant pattern is constantly decreasing as new patterns appear that show us the final shape that the overall pattern will take , as mentioned above.
3. In green and pink the columns of green and pink even numbers with the solutions of the conjecture , whose solutions tend to equality and their sum tends to equality with the solutions of the yellow even numbers in this size of numbers according to the distribution of prime numbers. This is the obvious finding that follows from the large prime number pattern and the Goldbach’s comet tail pattern that is automatically generated, in this number size, by the prime number distribution.
4. The other special patterns, number relations, the differentiations created in this basic pattern from one even number to another even number without however overturning this original basic pattern, but constantly changing it, are basic topics of the “Godbach conjecture” and not of the unity of the patterns of prime numbers.
In the next post the “holy grail” in the prime number theorem the basic problem.
“The periodic distribution matrix of prime numbers”.
“Riemann hypothesis”.
The Riemann hypothesis implies results for the distribution of prime numbers”
It has not been realized but the periodic distribution matrix of prime numbers, is the solution to other important theories .Such as the “universality effect”, the study of order numbers, the unique prime factorization, “ideal numbers” the logical numbers (p -adic numbers). All these theories pursue the same goal , to reconcile competing prime factors into a single set of prime factors. Unique prime factorization is a way of constructing a numerical system from fundamental building blocks. That is, as is the basis of the creation of the periodic distribution matrix of prime numbers.
Bibliography – Publications
“This publication is a minimal part of the whole work of “Theorem of Prime Numbers” and the copyright belongs to.
Yiannoulas Nikos
Kalambaka 5/7/2022